[サマリー]
・中央値や最頻値という指標を活用することによって、平均値だけでは見えてこない全体の傾向をつかむことができる
・目算での計算は非常に困難なため、Excel関数を活用し、中央値であれば「=median」、最頻値であれば「=mode」と入力すると便利である
以前、学校のテストや模試の分析方法として、平均点の弱点や標準偏差の活用について説明しました(詳しくはこちらの記事を確認下さい)。
今回は、平均値に加え、テストや模試の分析に使える中央値や最頻値という指標を説明したいと思います。結論を先に言ってしまうと、
平均値からでは全体の傾向が読み取れない場合があり、そういった時中央値や最頻値が非常に参考になる
ということなのです。
学校や塾における平均値,中央値,最頻値の活用
平均値の弱点
まず、平均点(平均値)の弱点について考えます。
平均点の弱点とはずばり、
外れ値に弱いこと
です。外れ値とはその他大勢のデータと大きくかけ離れたデータのことを指します。例えば模試で考えると、大勢の生徒が70点をとっているのに1人だけ30点をとっている場合、その30点というデータが外れ値になります。
平均点という指標は、この外れ値に弱いのです。
実際に先生方は実務で実感していると思いますが、クラスの中に1人点数が非常に低い生徒がいた場合、それだけで平均値が数点下がるようなことも多々ありますよね。模試でも同様です。全体として去年より学力層が高いにも関わらず、外れ値が複数あることによって平均点が去年以下になるようなケースも十分に考えられます。
そこで、平均点を算出する際は、他の指標も算出し、合わせて分析することが必須なのです。
そこで今回は、「中央値」「最頻値」について考えます。
中央値とは
では中央値から説明します。中央値とは、データを高い順もしくは低い順に並べた際、ちょうど中央に位置する値のことです。
実際に、具体例で考えてみたいと思います。10点満点のテストで考えていきましょう。

このテストの中央値を算出してみます。
中央値は、数値を順番に並べていった際の中央に来る値のことでしたね。では、並び替えてみましょう。

並び替えました。9人のテストなので、中央は5番目、つまりIさんの「4点」が中央値になります。ちなみに、データが膨大な時、この並び替えや計算は大変だと思いますので、Excelの関数を使ってください。セルに「=median」と入力し、データの範囲を選択すれば一瞬で中央値が表示されます。もし、データが偶数個しかなく中央が2つになってしまうなら、その2つの値の平均値が中央値になります。
では、この中央値の算出に何の意味があるのでしょうか。ズバリ、
中央値は平均値よりも全体の傾向を的確に表すケースがある
ということです。では、先ほどの例で平均値も計算してみます。

これを見ると、平均値は「5.2点」なのに対し、中央値は「4.0点」となり、1点以上の差が開いています。10点満点のテストなので、この差は大きいですね。
なぜ平均値が高く出ているかというと、C,E,Hさんの3人が非常に高い得点を取っている方です。これによって、6,7,8点あたりの層が1人もいないにも関わらず、平均点が高めに出ているのです。ある種の外れ値ともいえますね。
こういった時、中央値が役に立ちます。中央値はデータ数のど真ん中を取るため、「非常に高い点数」も「高い点数」も、同じ1人なのです。したがって、こういった外れ値があるような場合は、全体の傾向を知るうえで中央値が役に立ちますね。
では、最頻値についても計算してみましょう。最頻値を計算する効果は、中央値と同じく平均値では見えない全体の傾向を分析できるという点です。
最頻値とは
最頻値とは、データの中で最も多く出現している値のことです。では、先ほどのテストの例で考えてみましょう。
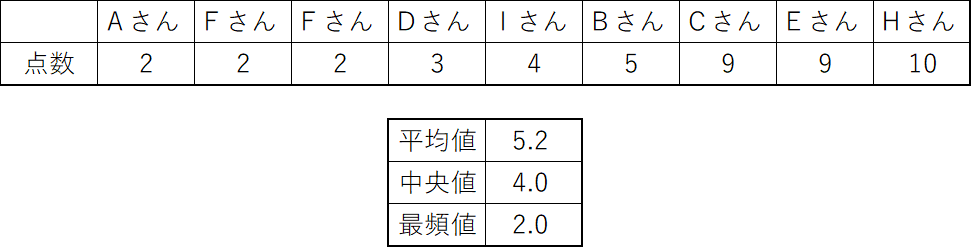
計算しました。このデータの量なら目算でも出せますが、Excelの関数なら「=mode」と入力し、データの範囲を選択してください非常に簡単に求められます。
今回の例では、最頻値、つまり最も多く出現した値は「2」ですね。この2という値も、平均値から大きく乖離していることが分かるかと思います。
平均値が5.2点なのに対し、最頻値が2.0点。これはつまり、
学力の二極化が示唆される
ということです。具体的には、下位層の多さが目立つということですね。
終わりに
以上、平均値、中央値、最頻値について、事例を確認しながら使い方を説明しました。平均値だけでは見えない傾向が見えてきたと思います。逆に、今まで平均値しか算出してこなかったという方は、他の指標も使わなければデータ全体の傾向は見えないんだということを理解して頂けたかと思います。
ぜひ、自校・自社で活用して頂ければと思います。
また、実務として業務改善を進めていくためには専門家の協力も重要となります。お悩みの際は、ぜひご相談ください。
学校の業務改善にお悩みの校長や管理職の方、こちらのホームページからのご相談お待ちしております。
「学校業務改善は経営コンサルタントにおまかせ下さい」
[まとめ]
・中央値や最頻値という指標を活用することによって、平均値だけでは見えてこない全体の傾向をつかむことができる
・目算での計算は非常に困難なため、Excel関数を活用し、中央値であれば「=median」、最頻値であれば「=mode」と入力すると便利である


