[サマリー]
・高低点法による固変分解はズレが大きくなることが多々あり、スキャッターチャート法はその欠点を解消した手法である
・スキャッターチャート法を数学的に行うのが最小二乗法であり、正確性・納得感の高い固変分解の手法である

固変分解には様々なやり方があります。その中でも代表的なものが高低点法や最小二乗法、そして最小二乗法の出発的手法であるスキャッターチャート法です。
今回は、この3つの方法について違いを考えながら説明していきます。
固変分解の3つの手法
そもそも固変分解とは?
固変分解とは、ある特定の費用を固定費と変動費(率)に分解することを指します。例えば、下図のような費用分布を考えてみましょう。
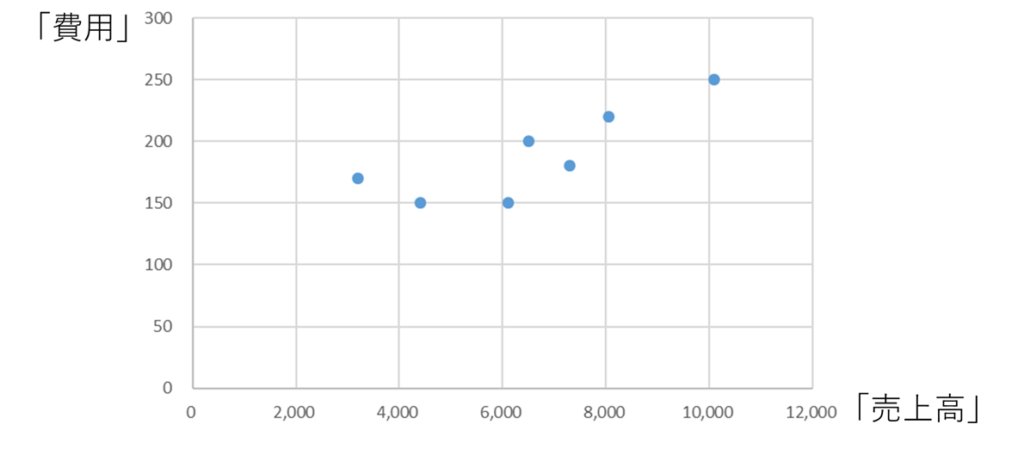
プロットが右肩上がりに並んでいますが、完全な比例関係になっているわけでもなく、変動費と言い切ることはできませんね。こういった時、どの部分を固定費とみなして、どの部分を変動費とみなすかが重要になってきます。
ここで、「どのようにみなすか」というのは、グラフ上で「どのように近似線を引くか」と同じ意味になります。例えば、
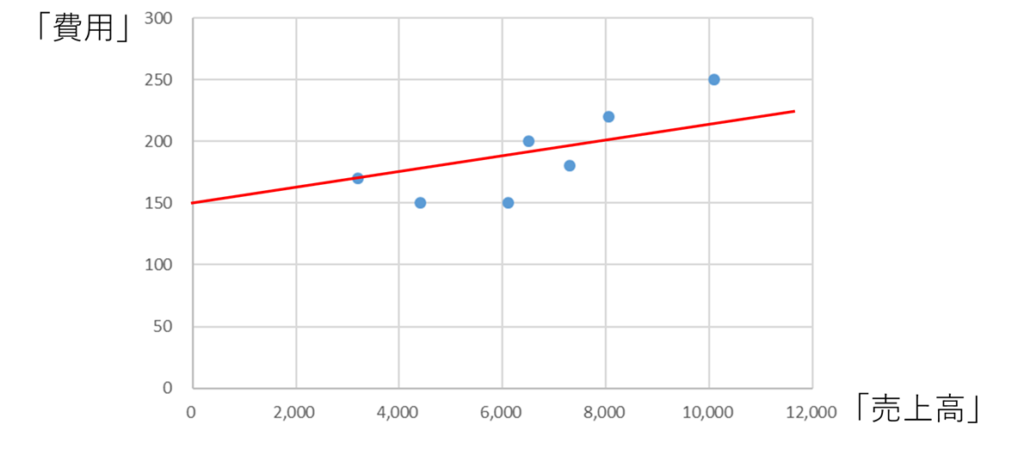
このように近似線を引いたなら、固定費は150円
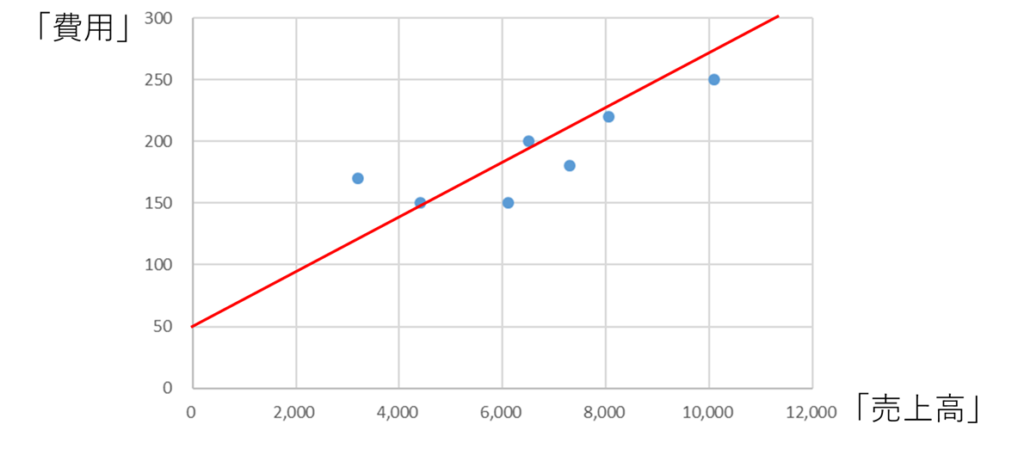
このように近似線を引いたなら、固定費は50円となります
「なぜ固定費が50円になるんだろう」と思った方も多いかと思いますが、グラフ上で固定費は切片にあたります。定義より売上高がゼロの時に発生している費用が固定費なので、切片(売上高がゼロのところ)にあたる50円が固定費となるのです。
つまり、どのように近似線を引くかということがそのまま、どのように固変分解を行うかということになるのです
ちなみに、グラフの傾きは変動費率にあたります。変動費率とは売上高に対して費用がどのような割合で増えるかなので、傾きの定義そのものだからです。
少し説明が長くなりますが、冒頭で固変分解を「固定費と変動費(率)」に分けるといったのはこれが理由です。変動費率と固定費は常に一定なのに対し、変動費は売上高によって変化してしまいます。よって、「この費用科目の変動費は〇円だ!」というのは意味が薄く、「この費用科目の固定費は〇円、変動費率は×%です」という分析の方が意味があるといえます。
では実際に、固変分解の手法について説明してきます。
固変分解の手法
高低点法
高低点法とは、一番売上高が高い時の項目と、低い時の項目のみを使って固変分解を行う方法です。
実際に具体例を見ていきましょう。例えば、このように発生する費用があったとします。

このような費用に対して高低点法で固変分解を行う場合、注目するのはこの2つだけです。

売上高が最も高い時の費用2,400円と、売上高が最も低い時の費用1,200円のみに注目して固変分解を行うのです。極端なやり方ともいえますね。
では実際に、高低点法を使って固変分解をするとどのようになるのか、計算式から説明します。
まず考えるのは、費用と固定費・変動費率の関係についてです。これらの関係は、以下のような式で表すことができます
「費用=変動費率×売上高+固定費」
このような式です。なぜこのような式になるかですが、費用は変動費+固定費ですよね。ここで変動費は定義より、変動費率×売上高と表すことができます。
したがって、上のような式になるのです。
(ここで数学ができる方は、グラフ・一次関数との関係を押さえておくと非常に便利です。グラフ上では固定費は切片、変動費率は傾きを表しているので、上記の式が一次関数の公式y=ax+bになっていることがお分かりいただけるかと思います)
あとは、「高」と「低」の2点についてこの式に代入するだけで、固定費と変動費(率)を求めることができます。
〇「高」点について
売上高が一番高いのは100,000円で、その時の発生費用が2,400円でした。
これを式に代入すると、
2,400=変動費率×100,000+固定費 …①式
となります。
〇「低」点について
売上高が一番低いのは40,000円で、その時の発生費用が1,200円でした。
これを式に代入すると、
1,200=変動費率×40,000+固定費 …②式
となります。
では、①式と②式から、固定費と変動費率を求めます。
①式:2,400=変動費率×100,000+固定費
②式:1,200=変動費率×40,000+固定費
最も簡単なのは、①式から②式を引いて、固定費を消去するやり方です。
①式から②式を引くと、
1,200=変動費率×60,000
になるので、変動費率=2% と求めることができました。
ここまで求められれば、この値を①式などに代入して、固定費=400円 という結果も求めることができます。
これが高低点法による固変分解です。最後に、グラフ上での表現を確認してみます。
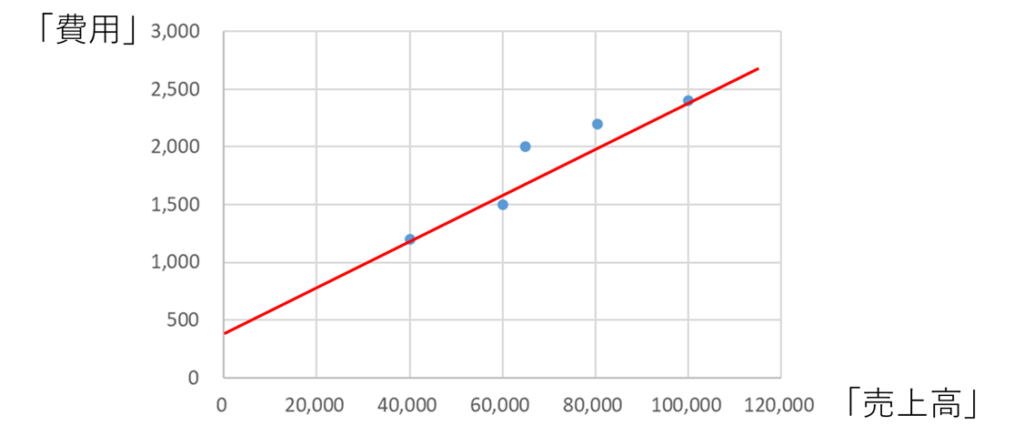
これが高低点法による固変分解です。確かに、近似線が売上高が一番高い時の費用(右端)と、売上高が一番低い時の費用(左端)を通っていることがわかると思います。逆に言えば、それ以外のプロットは全て無視するというのが高低点法の最大の特徴といえます。
ここで、1つ当然の疑問が湧いてくるかと思います。
無視する要素が多すぎる!
正論ですね。高低点法では2つのデータしか計算に用いません。そこで当然、他のデータも考慮した固変分解をするべきだという意見がでてきます。
それを解消するのが、ここから紹介するスキャッターチャート法なのです。
※高低点法について更に詳しく知りたいという方は、こちらの記事をご確認ください。
→高低点法による固変分解のやり方
スキャッターチャート法
スキャッターチャート法による固変分解とは、妥当と思われる固変分解を目分量で行う手法です。
「目分量!?」と驚いた方もいらっしゃるかもしれませんが、目分量です。
では、具体例を見ていきましょう。先ほど高低点法を使って固変分解をした費用のデータを使用してみます。
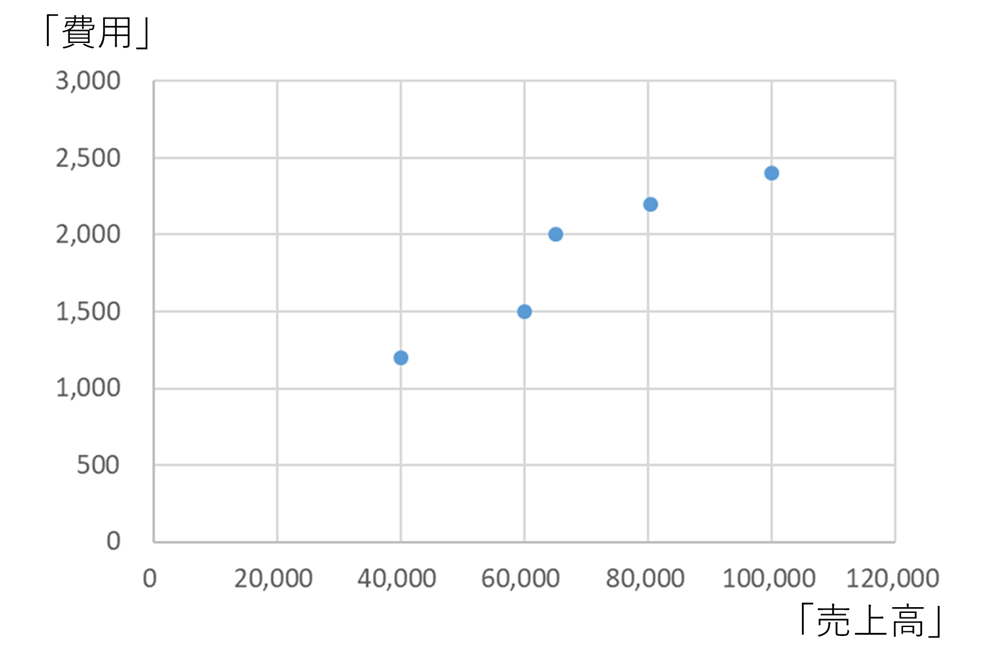
では、スキャッターチャート法による固変分解をしてみましょう。
例えばこんな感じです。
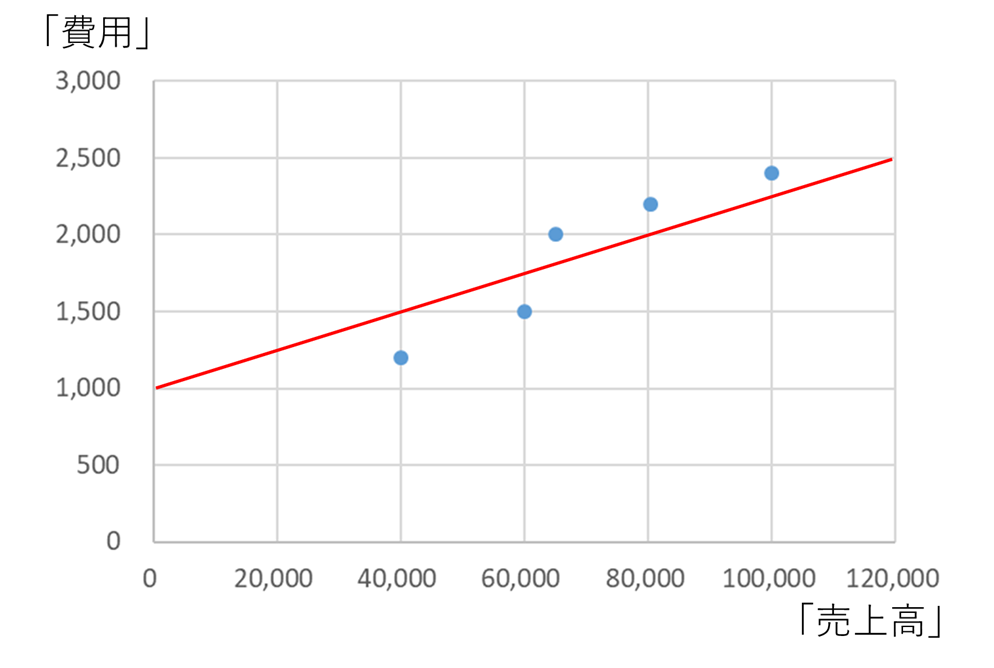
できました。もちろん目分量なので他の固変分解の仕方(近似線の引き方)も何通りも考えられます。
「こんなんで大丈夫なのか」と思った方も多いかと思いますが、一般的にスキャッターチャート法は高低点法より正確であることが知られています。
なぜかといえば、スキャッターチャート法が目分量ではあるものの全てのプロットを考慮するのに対し、高低点法は2つのデータしか考慮しないため大きなズレが生じやすいのです。
例えば、こんな費用を固変分解する際、高低点法の弱点が露呈します。
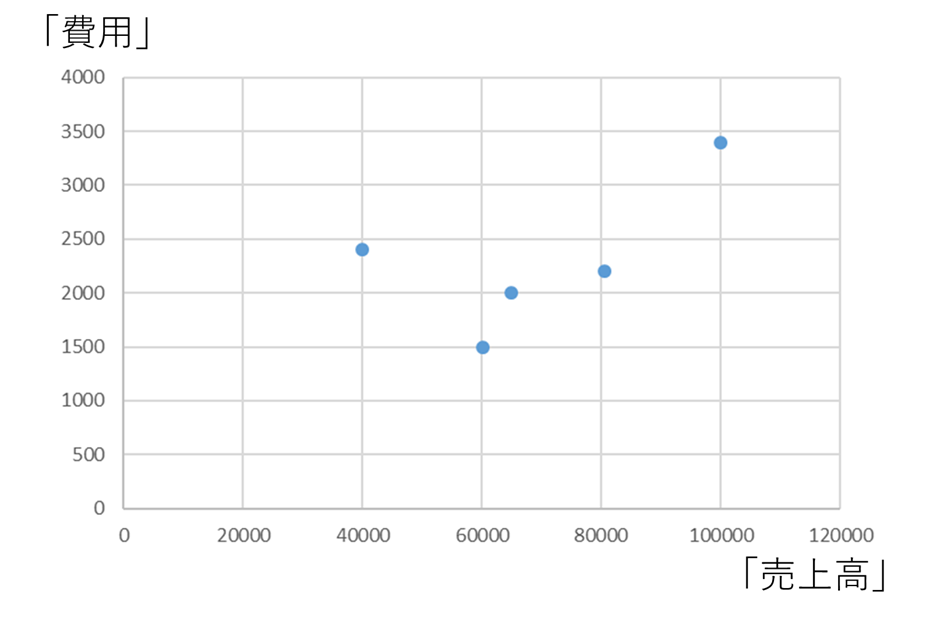
売上高が最高の時の費用と最低の時の費用が例外的な値となっている(外れ値になっている)ようなケースです。このような場合に、高低点法とスキャッターチャート法による固変分解を行った際の比較をしてみるとこのようになります。
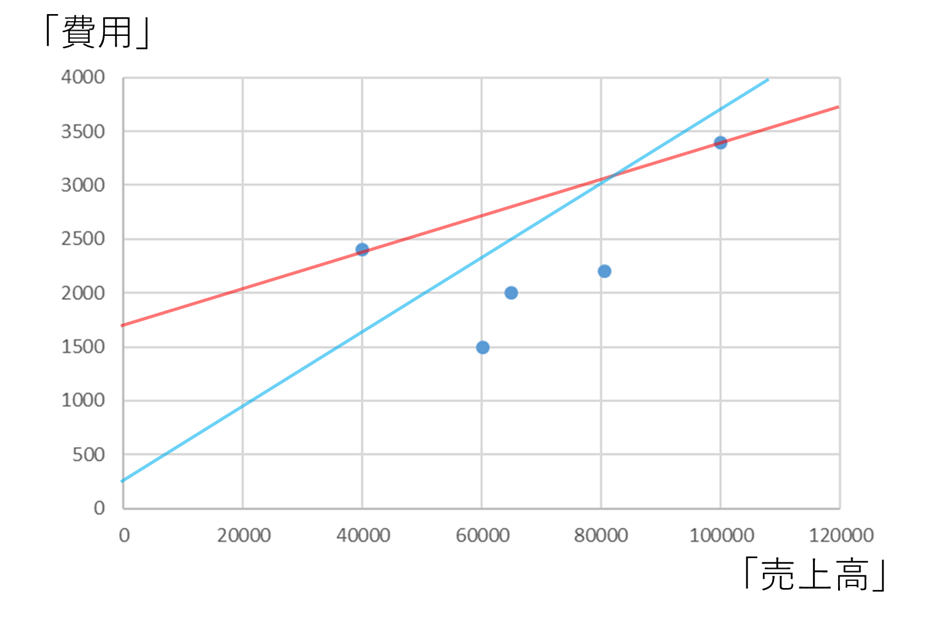
赤線が高低点法、青線がスキャッターチャート法による固変分解です。
赤線は2点しか考慮しないため残りの3点から非常に大きくかけ離れた近似線となってしまいます。一方、スキャッターチャート法は弱くはありますが全体を意識した近似線を引くことができます。
これが、スキャッターチャート法による固変分解の強みといえます。
しかし、目分量による固変分解というのは少し違和感がありますよね。実は、スキャッターチャート法を数学的に行う手法が存在します。それが「最小二乗法」なのです。
※スキャッターチャート法についてさらに詳しく知りたいという方はこちらの記事もご確認ください。
→固定費と変動費の分解「固変分解」とは?スキャッターチャート法の紹介
最小二乗法
最小二乗法とは、複数のデータの組を与えられたとき、そのデータの関係性を表す最もふさわしい関数を数学的に求める手法です。
最小自乗法と書くこともあります。
定義は少し分かりづらいですが、スキャッターチャート法を数学的にやるというイメージがそのまま当てはまります。
また、グラフの近似から見ていきましょう。
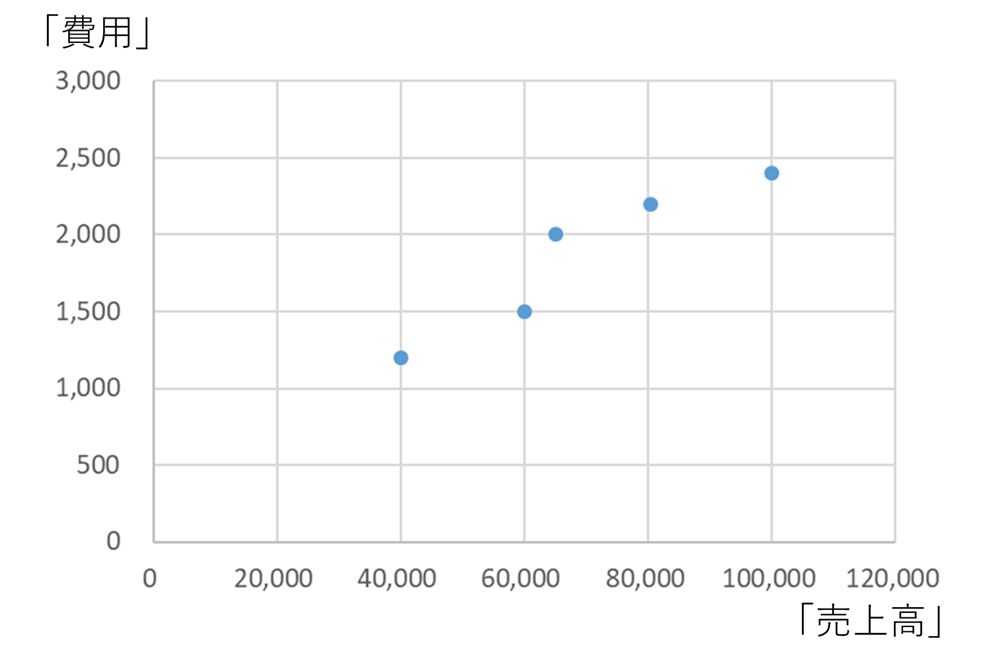
このような費用のデータがあるとします。先ほどと同じものです。
これを最小二乗法を使って固変分解したのが、
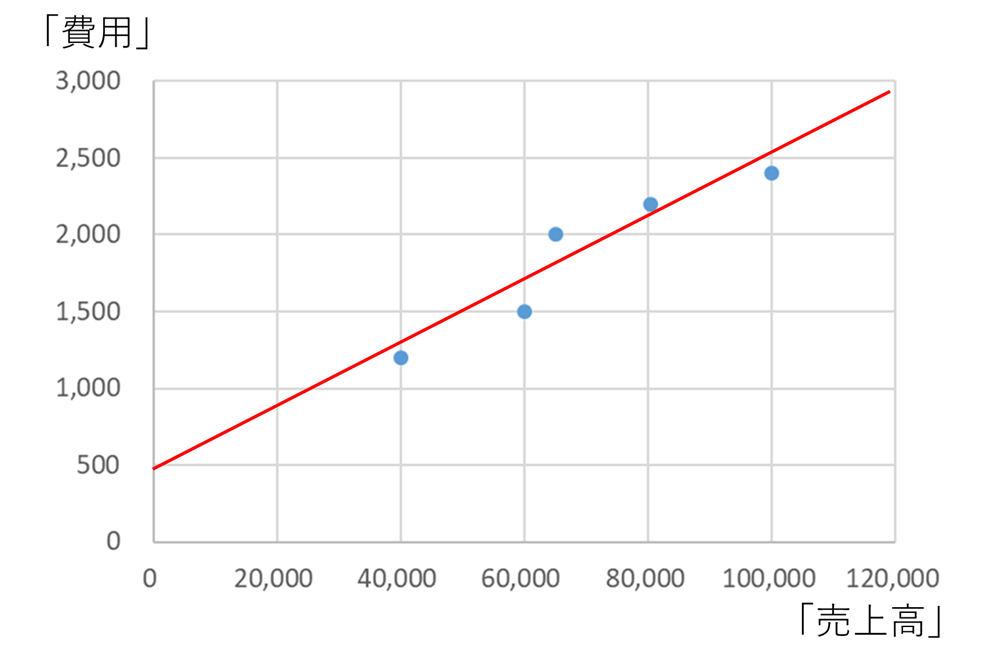
こちらです。確かに、全てのプロットから大きなズレがない納得感の高い固変分解になっているかと思います。
そもそも最小二乗法は、それぞれのプロットと近似線のズレの総和が最小になるような近似線を引くように計算する手法です。したがって、全てのプロットを考慮しつつも、目分量ではない確からしさの高い固変分解を行うことができるのです。
問題はこの最小二乗法のやり方(実際の近似線の引き方)ですが、エクセルを使って本当に簡単に行うことができます。この記事では概要の説明に留めますので、エクセルを使った最小二乗法による固変分解のやり方は下の記事を確認してください。
→エクセルを使った最小二乗法による固変分解とは
→最小二乗法によるエクセルの回帰分析を使った固変分解
※上の記事の方がより簡単なやり方になっています。下の記事はデータ分析というツールを使ったやり方ですが、固変分解の結果の品質は変わりません。
以上、固変分解のやり方について、高低点法・スキャッターチャート法・最小二乗法という3つの方法を実例を見ながら説明しました。結論として、パソコン等の計算ができる環境があれば最小二乗法が最も正確に固変分解をできるということになります。実務で固変分解をされる際は、かける労力・時間と得られる結果の効果を天秤にかけ、手法を選択することが重要といえます。
[まとめ]
・高低点法による固変分解はズレが大きくなることが多々あり、スキャッターチャート法はその欠点を解消した手法である
・スキャッターチャート法を数学的に行うのが最小二乗法であり、正確性・納得感の高い固変分解の手法である
会社経営や財務にお悩みの経営者や管理職の方、こちらのホームページからのご相談お待ちしております。
-1024x384.png)
-1024x386.png)





