[まとめ]
・ 最小二乗法とは、複数のデータの組を与えられたとき、そのデータの関係性を表す最もふさわしい関数を数学的に求める手法です。
・エクセルを使うことによって、非常に簡単に最小二乗法による固変分解を行うことができる
会社・企業の管理会計において、特定の費用を変動費と固定費に分解することを固変分解といいます。固変分解には様々な手法がありますが、その中でも代表的なものの1つに「最小二乗法」があります。
今回は、この固変分解の手法である最小二乗法について、考え方やエクセルを用いたやり方などを説明していきます。
エクセルを使った最小二乗法による固変分解
そもそも固変分解とは?
固変分解とは、特定の費用を固定費と変動費(率)に分解することをいいます。
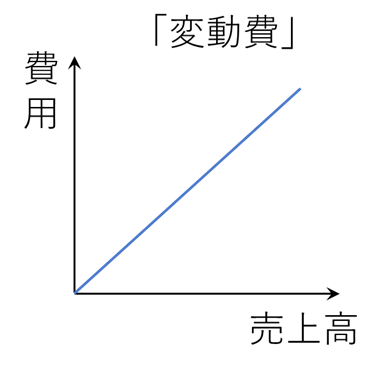
まず、変動費とは売上高と比例関係にある費用のことをさします。例えば、売上高が2倍になれば、費用も2倍になるというとき、その費用を変動費といいます。
変動費をグラフで表すと、このような形になります。(最小二乗法の理解にはグラフが非常に重要なので、この段階からグラフのイメージを大切にして頂ければと思います)
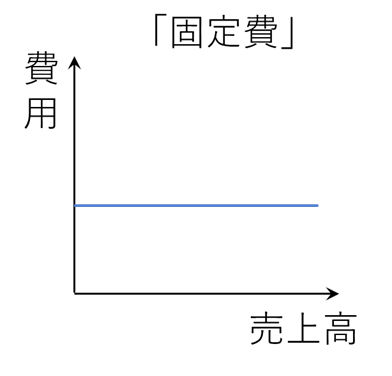
次に固定費とは、売上高が増減しても金額が変わらない費用のことを指します。例えば、売上高が2倍になっても費用の大きさが一定で変わらないとき、その費用を固定費といいます。
固定費をグラフで表すとこのような形になります。
これが変動費と固定費の定義です。しかし実際には、このように変動費と固定費に綺麗に分けることができるというわけではありません。「これは変動費っぽいけど完全には変動費じゃないよな…」というようなケースも非常によくあります。
例えば、下のような例を考えてみましょう。
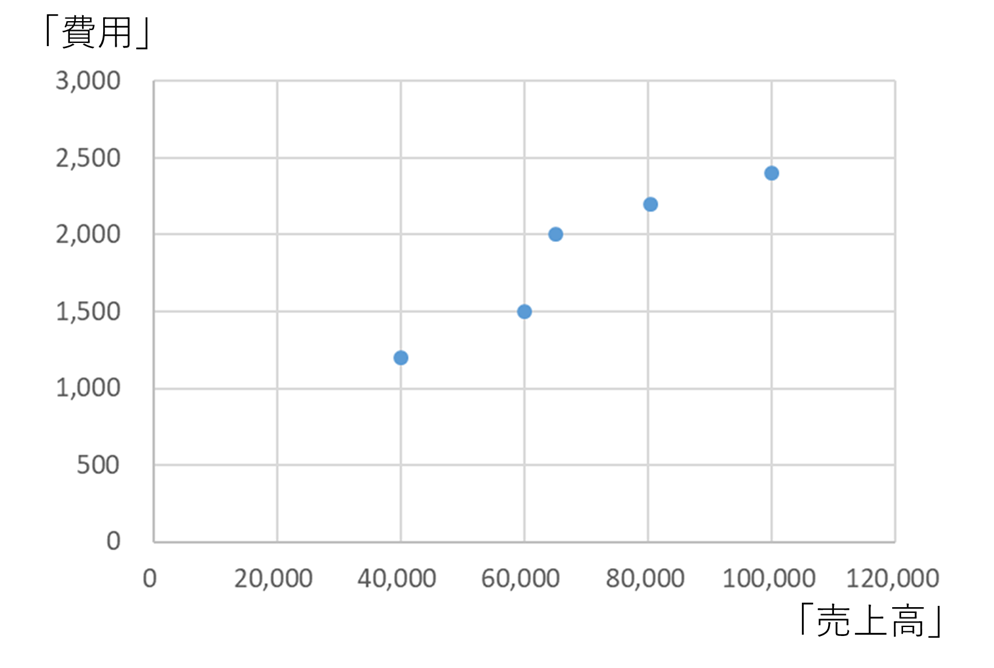
なんとなく変動費っぽいですが、完全に費用が売上高に比例している(=変動費)というわけでもなさそうですよね。
こういった時、どのように変動費部分をみなすか、どのように固定費部分をみなすかという作業が必要になってきます。この費用を、変動費と固定費の足し合わせと考えるということです。
この作業のことを固変分解といいます
例えば、このような形で費用をみなすとしましょう。
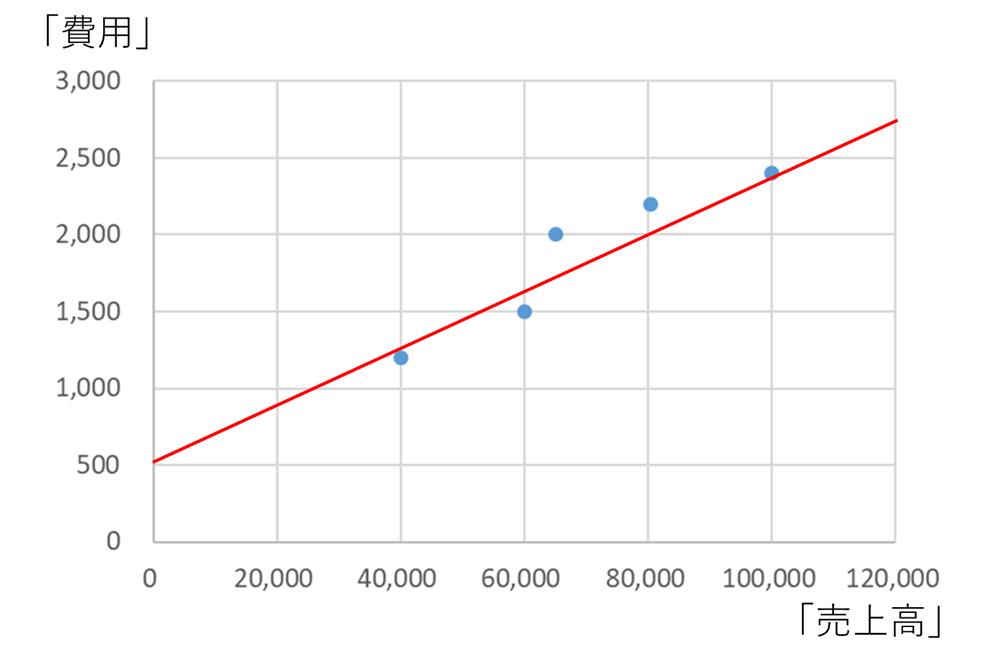
このように費用をみなした場合、固定費は500円、それ以外の部分は変動費となります。固定費は売上高に関係なく発生する費用なので、売上高が0円のときの費用500円が固定費と分かります(つまりグラフの切片を確認すればよいということです)。
このように、固変分解は費用をグラフ上に落とした上で、グラフをどのようにみなすか(近似するか)という作業のことなのです。
ちなみに、変動費に関しては売上高によって変化してしまうため、固変分解においては「変動費率」を算出するのが一般的です。変動費率とは売上高に対する変動費の割合のことで、グラフの傾きにあたります。この変動費率なら売上高に対しても一定なので、「固定費〇〇円」「変動費率〇〇%」という風に具体的に算出することができます。
上記の例で言えば、「固定費500円」「変動費率1.875%」となります。(グラフの傾きが変動費率です)
「少し分からないな…」と思った方は、こちらの記事で詳しく説明しているので、ぜひご確認ください。
→変動費とは?固定費との違いや変動費率の意味を紹介
→固定費と変動費の分解「固変分解」とは?スキャッターチャート法の紹介
(上の記事は変動費と固定費について、下の記事は切片や傾きについて詳しく説明しています)
それでは、本題の最小二乗法による固変分解を説明していきます。
最小二乗法とは?
最小二乗法とは、複数のデータの組を与えられたとき、そのデータの関係性を表す最もふさわしい関数を数学的に求める手法です。
最小自乗法と書くケースもあります。
定義は少し硬い言い回しなので、またグラフで見ていきましょう。
先程説明したような、固変分解におけるグラフの近似から見ていきましょう。

上図は先ほどと同じ図です。費用と売上高の関係を表しています。
この費用をどのように固変分解するか(つまり近似線を引くか)というときに、

このように近似線を引くのか、
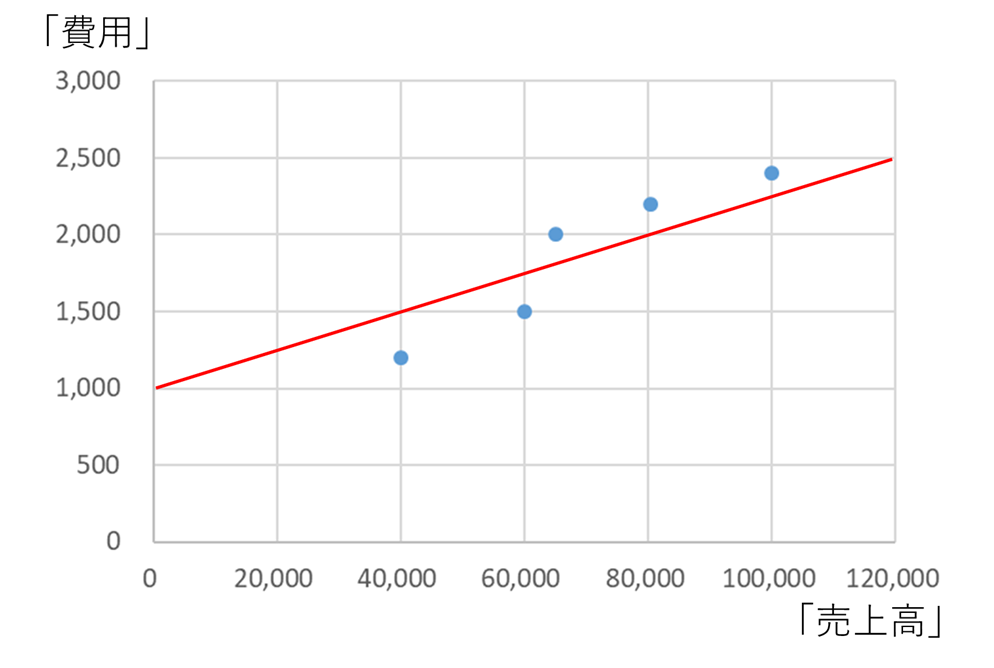
このように近似線を引くのか、どちらが正しいのでしょうか。
それぞれ、上のような固変分解では固定費500円、下のような固変分解では固定費1,000円となってしまい、全く異なる結果となります。
結論、どちらも正しいのです
固変分解には絶対的に統一された手法はなく、自分が思う手法に沿って固変分解を行うことになります。ちなみに、上図のように目分量で固変分解を行う手法をスキャッターチャート法といい、歴とした固変分解の手法です。
しかしこれでは、納得性に欠けますよね。なにか理論的な固変分解の手法が欲しいところです。
ここで、最小二乗法の登場です。最小二乗法は固変分解(グラフの近似線)を数学的に求める手法です。「目分量で求めた」というよりよっぽど納得感が高いですよね。
それではどのように求めるのかですが、エクセルを使うと非常に簡単に最小二乗法による固変分解を行うことができます。本当に簡単です。
ということで、ここからエクセルを使った最小二乗法による固変分解のやり方を紹介していきます。
エクセルを使った最小二乗法による固変分解
エクセル上の操作
まずはデータを用意してください。それをグラフ上にプロットした状態をスタートとします。例えば、このような形です。

次にグラフを選択した状態で、タブ「デザイン」→グラフ要素を追加→近似曲線→線形 の順番にクリックしてください。
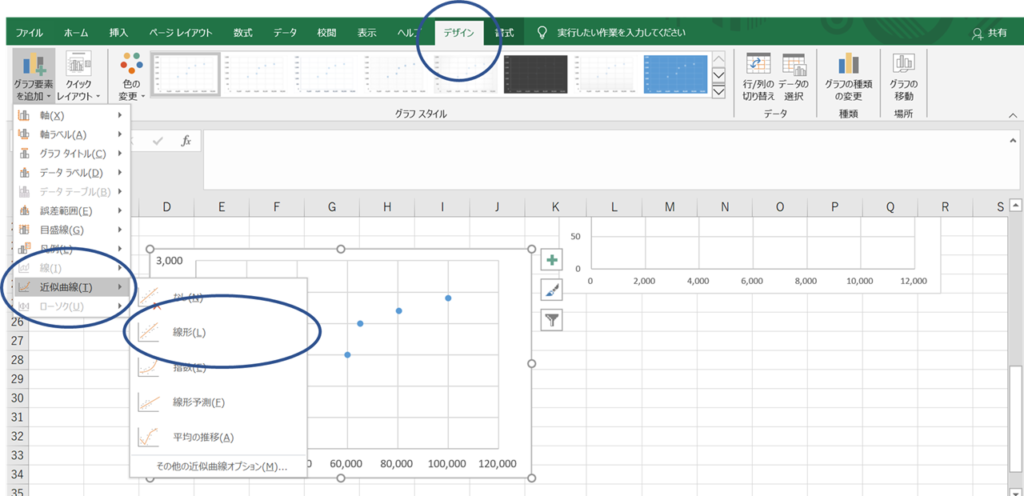
すると、このような近似線が引かれます。
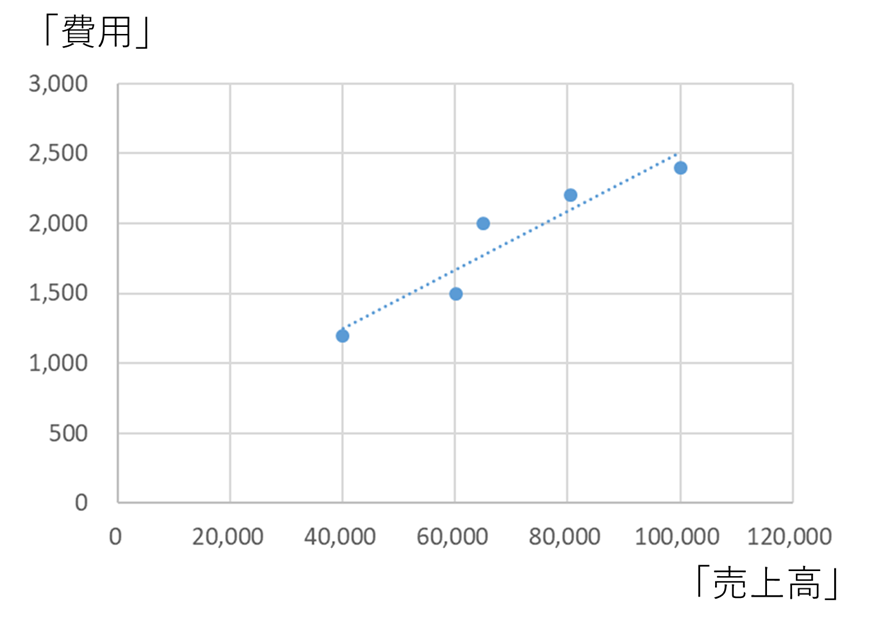
これだけで固変分解ができてしまいました。本当に簡単ですね。
ただこれだけだと、具体的に固定費○○円、変動費率○○%ということが分からないので、最後にグラフの解釈について説明します。
結果の解釈
先程の状態から近似線をダブルクリックし、右側に出てくるメニューの中から「グラフに数式を表示する」にチェックを入れてください。すると、グラフ上に数式が表示されます。
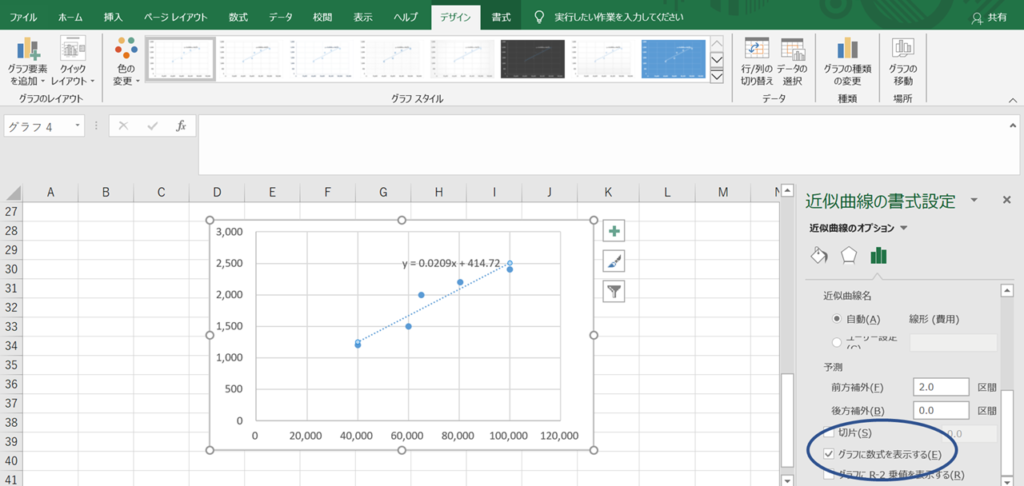
この例で言えば、
「y=0.0209x+414.72」
という式が出てきました。ここで、1次関数の公式を思い出します(数学が苦手な方、なんとか中学の授業を思い出しましょう…!)。
1次関数の公式は「y=ax+b」で、aがグラフの傾き、bが切片を表していました。
今回の例で言えば、グラフの傾きは0.0209、切片が414.72です。
そしてこの記事の前半で説明したように、グラフの傾きは変動費率を、切片は固定費を表しています。
つまりこの結果から、
変動費率2.09%、固定費414.72円
ということがわかるのです。変動費率は%表示なので、グラフの結果に100を掛けます。
先程目分量で固変分解をした結果を思い出すと、変動費率1.875%、 固定費500円 となっていました。案外、目分量も最小二乗法と近い結果になってるという見方もできますね。しかし、理論的な手法で、さらに簡単に求めることができるということに最小二乗法のメリットがあるのです。
以上、エクセルを使った最小二乗法による固変分解のやり方について説明しました。非常に簡単に求めることができますので、ぜひ活用して頂ければと思います。
(ちなみに、エクセルを使った固変分解には「回帰分析」というもう一つのやり方があります。ご興味のある方はこちらの記事をご確認ください。→最小二乗法によるエクセルの回帰分析を使った固変分解)
[まとめ]
・ 最小二乗法とは、複数のデータの組を与えられたとき、そのデータの関係性を表す最もふさわしい関数を数学的に求める手法です。
・エクセルを使うことによって、非常に簡単に最小二乗法による固変分解を行うことができる
会社経営や財務にお悩みの経営者や管理職の方、こちらのホームページからのご相談お待ちしております。
-1024x384.png)
-1024x386.png)





