[サマリー]
・ エクセル分析ツールを活用することで、非常に簡単に回帰分析を行うことができる
・回帰分析結果の「切片」は固定費を、「傾き」は変動費率をそれぞれ表している

会社・企業の管理会計において、特定の費用を変動費と固定費に分解することを固変分解といいます。固変分解には様々な手法がありますが、その中でも代表的なものの1つに「最小二乗法」があります。
最小二乗法による固変分解はエクセルを使って非常に簡単に行うことができますが、やり方が2通りあります。
今回はそのうちの1つである「回帰分析を使った最小二乗法による固変分解」を説明していきたいと思います。
エクセルの回帰分析による固変分解
そもそも固変分解とは?
固変分解とは、特定の費用を固定費と変動費(率)に分解することをいいます。
まず、変動費とは売上高と比例関係にある費用のことをさします。例えば、売上高が2倍になれば、費用も2倍、売り上げが3倍になれば費用も3倍といったとき、その費用を変動費といいます。
変動費をグラフで表すと、このような形になります。固変分解の理解にはグラフのイメージが非常に重要なので、しっかり覚えてください。
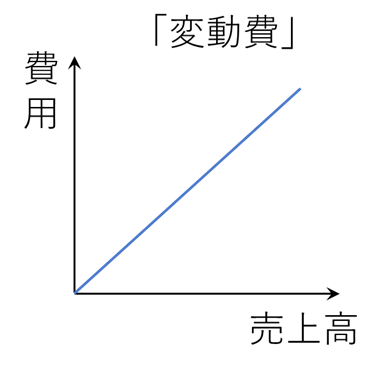
次に固定費とは、売上高が増減しても金額が変わらない費用のことを指します。例えば、売上高が2倍になっても費用の大きさが一定で変わらないとき、その費用を固定費といいます。
固定費をグラフで表すとこのような形になります。
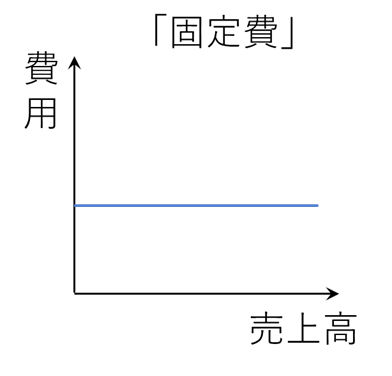
以上が変動費と固定費の説明です。しかし実務においてには、このように変動費と固定費に綺麗に分けることができるというわけではありません。「これは変動費っぽいけど完全に比例しているわけではないよな」というようなケースも非常によくあります。
例えば、下のような例をみてみます。
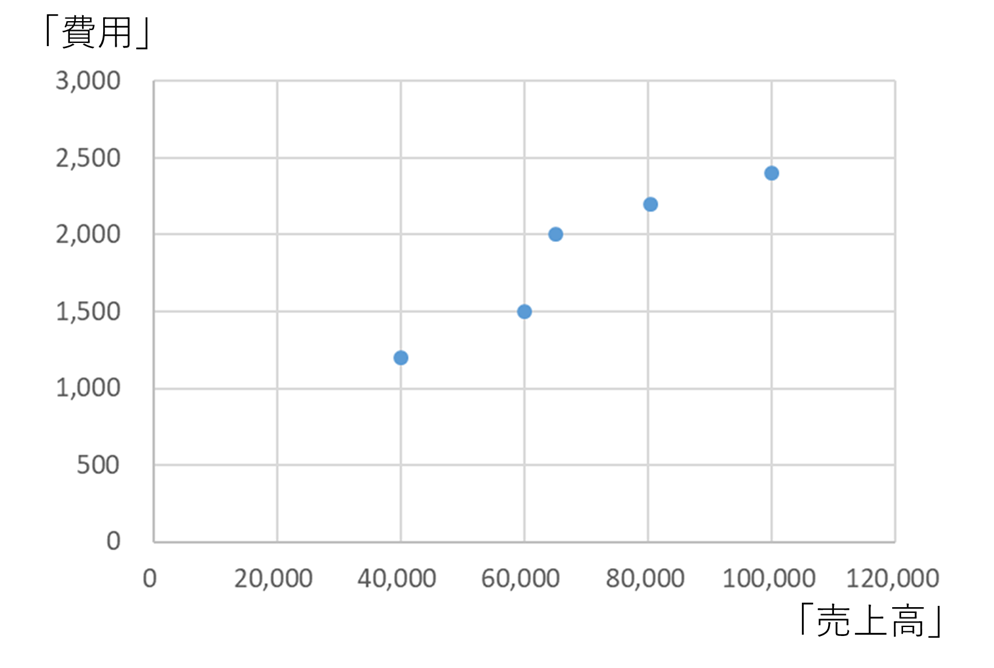
変動費に近いプロットになっていますが、完全に費用が売上高に比例している(=変動費)というわけでもないですよね。かといって、固定費ではないなというようなイメージだと思います。
このような場合にどの部分を変動費とみなすか、どの部分を固定費とみなすかという作業が必要になってきます。
この作業こそが固変分解なのです
例えば、このような形で費用をみなすとしましょう。
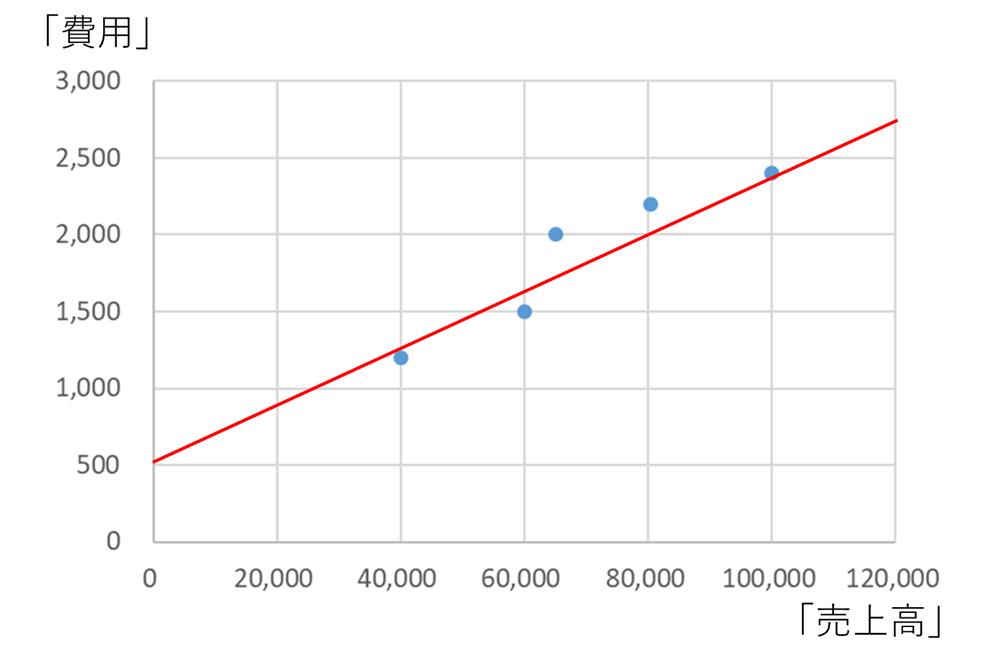
上図のように費用をみなした場合、固定費は500円、それ以外の部分は変動費となります。固定費は売上高に関係なく発生する費用なので、売上高が0円のときの費用500円が固定費と分かります(つまりグラフの切片を確認すればよいということです)。
つまり固変分解とは、グラフ上で費用をどのようにみなすか(近似するか)という作業のことなのです
ちなみに、変動費に関しては売上高によって変化してしまうので、固変分解においては「変動費率」を算出するのが一般的です。
変動費率とは売上高に対する変動費の割合のことで、グラフでいうところの傾きにあたります。この変動費率なら売上高に対しても一定なので、「固定費〇円」「変動費率〇%」というように具体的に算出することが可能です。
上記の例で言うと、「固定費500円」「変動費率1.875%」となります。(ここで、グラフの傾きが変動費率を表しています)
「少し難しいな…」と思った方は、こちらの記事で詳しく説明しているので、ぜひご確認ください。
→変動費とは?固定費との違いや変動費率の意味を紹介
→固定費と変動費の分解「固変分解」とは?スキャッターチャート法の紹介
(上の記事では変動費と固定費について、下の記事では切片や傾きについて詳しく説明しています)
それでは、本題の最小二乗法による固変分解を説明していきます。
最小二乗法とは?
最小二乗法とは、複数のデータの組を与えられたとき、そのデータの関係性を表す最もふさわしい関数を数学的に求める手法です。
最小自乗法と書くこともあります。
非常に簡単なイメージとして、先ほどの固変分解の直線を思い出してください。直線の引き方(=固変分解のしかた)は様々なケースが考えられますが、数学的にふさわしい直線を引くというのが最小二乗法になります。
例えば、最小二乗法によって直線を引く(固変分解する)と、下のような結果になります。
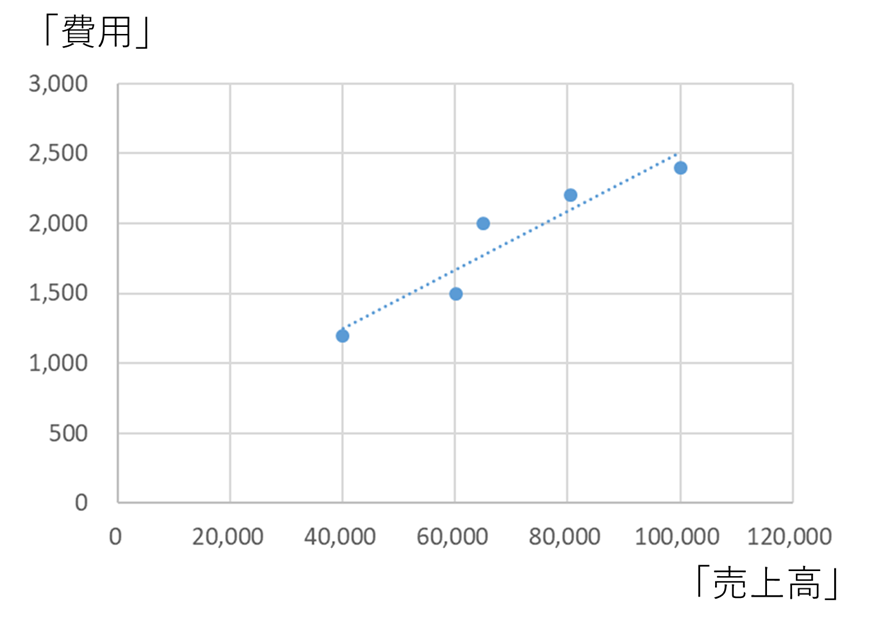
直線が伸びきっていないので結果が少しわかりにくいですが、たしかにそれぞれのプロットから外れすぎていないような、納得性の高い結果になっていることがわかります。(ちなみに上の図の場合、固変分解の結果としては 変動費率2.09%、固定費414.72円になっていました)
このように固変分解の手法として最小二乗法を使うことで、納得性の高い固変分解を行うことができるのです。
それではここから、エクセルを使った最小二乗法のやり方を紹介していきます。
記事の冒頭で説明したようにエクセルを使ったやり方は大きく2つあり、
・グラフの機能を使ったやり方
・回帰分析(エクセル分析ツール)を使ったやり方
この2つです。今回は、2つ目の回帰分析を使ったやり方を説明していきます。
1つ目のグラフの機能を使ったやり方についてはこちらの記事で説明しているので、気になる方はご確認ください。→エクセルを使った最小二乗法による固変分解とは
エクセルの回帰分析を使った固変分析
データの準備
まずは固変分解したいデータを準備します。例えば、このようなデータだとしましょう。
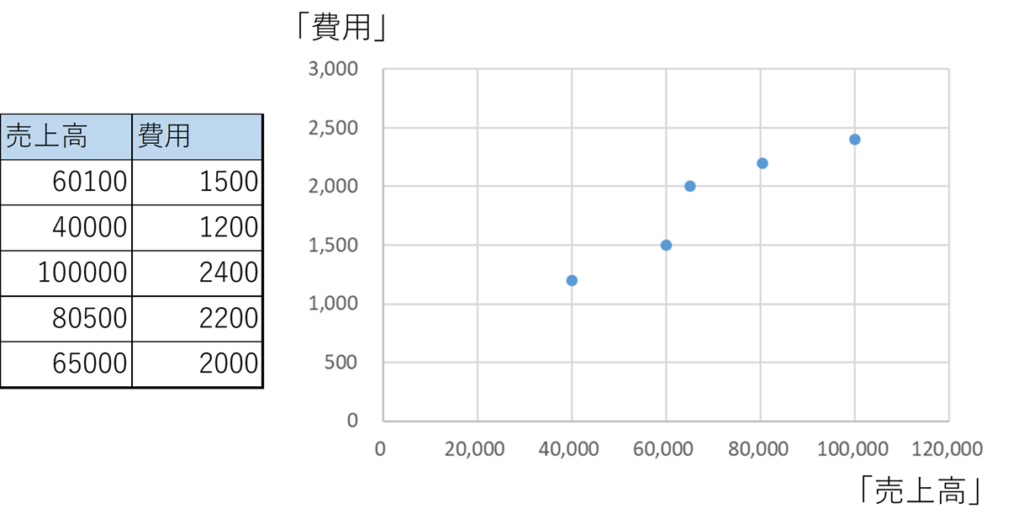
目的は、このデータの費用を固変分解することです。
次に、必要な分析ツールを導入していきます。
分析ツールの導入
ここからはエクセルの画面で説明していきます。
まず、エクセルの「ファイル」→「オプション」→「アドイン」を選択して下さい。すると、このような画面がでてきます。
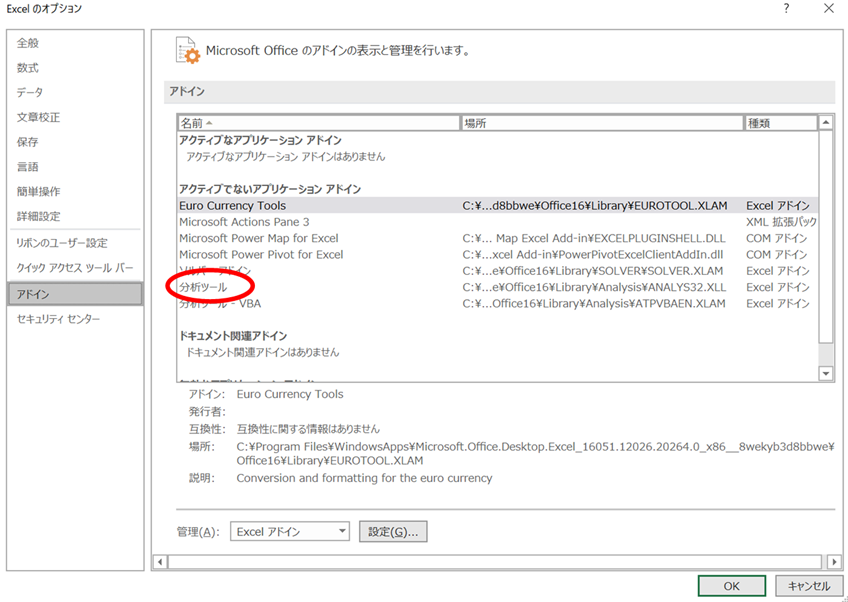
少し見にくいですが、真ん中の赤で囲った「分析ツール」を選択し、「設定」→「分析ツール」にチェックを入れる→「OK」の順番にクリックしてください。
すると、エクセルの「データ」のタブの一番右に、「分析」という欄が出現します。これで準備は終了です。
回帰分析の実行
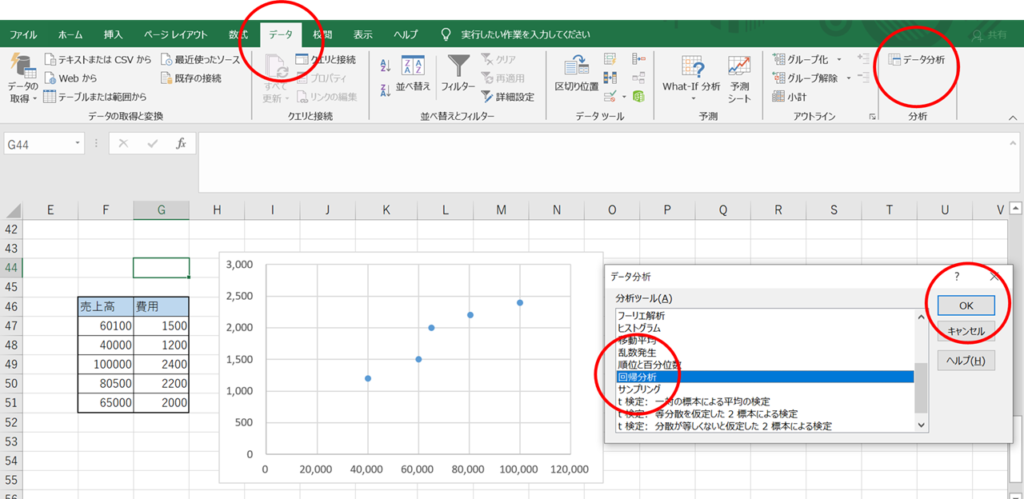
ここからは実際に、回帰分析を行っていきます。
まず、「データ」タブ→ 「データ分析」→「回帰分析」→「OK」の順番にクリックしてください。
すると、下のような画面がでてきます。
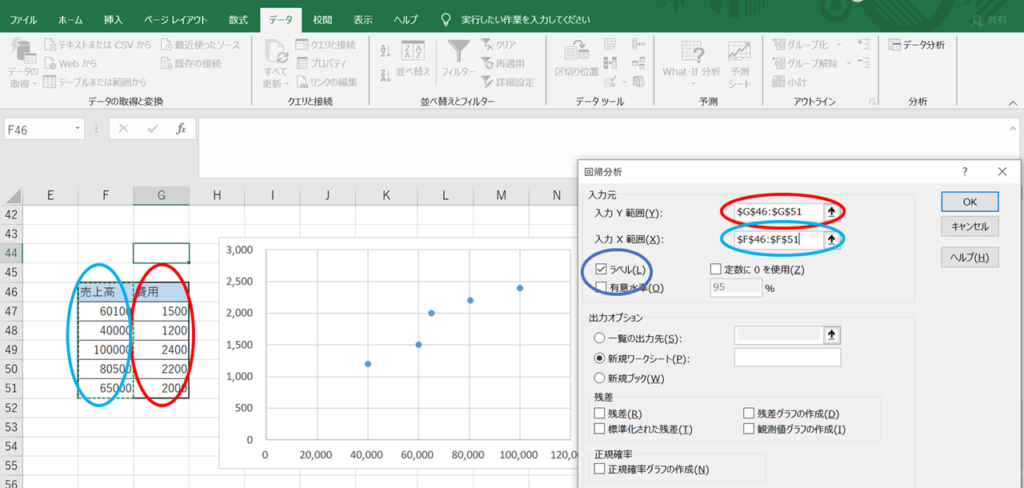
ここで、「入力Y範囲」の部分に費用の数値を、「入力X範囲」の部分に売上高の数値を指定してください。赤色と水色で入力部分を対応させているので、参考にしてください。範囲には「費用」「売上高」という文字の部分を入れておくとよいと思います。
さらに、「ラベル」にチェックマークを入れてOKをクリックします。
その結果、下図のような結果が出力されます。
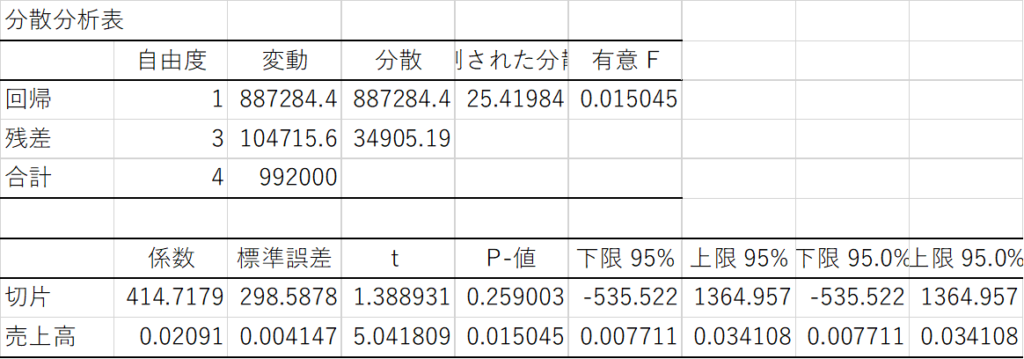
これで回帰分析は終了です。これを解釈するだけで、固変分解の結果を知ることができます。
結果の解釈
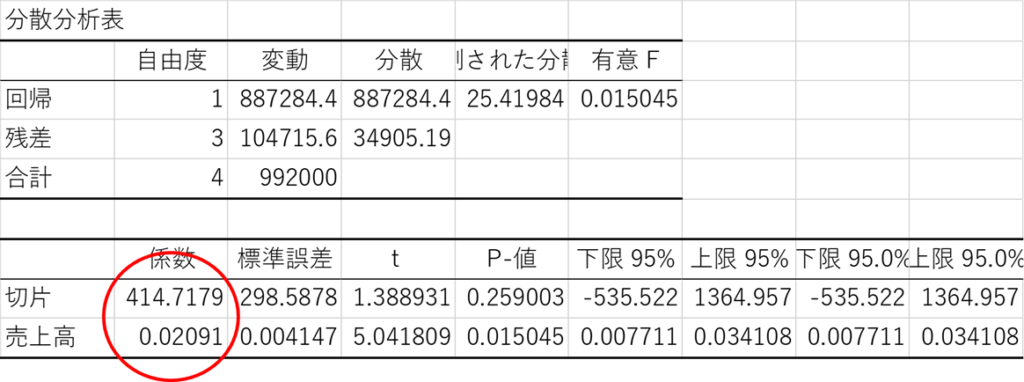
では、結果の解釈を行いましょう。
細かい部分を見ればキリがありませんが、注目するのは上図で〇がついている「係数」の部分です。
ここを見ると、「切片414.7179」「売上高0.02091」となっています。
結論から言うとこの結果は、
固定費414.7179円、変動費率2.091%
ということを表しているのです。
ここで、記事の中盤で説明したグラフ上での固定費と変動費率の位置付けを思い出します。グラフ上では、切片が固定費を、傾きが変動費率を表していました。数学が分かる方は1次関数(グラフを表す式)をイメージしてください。y=ax+bのaが変動費率、bが固定費を表しています。
つまり、回帰分析の結果は近似直線の「切片」と「傾き」を表しているので、その結果がそのまま「固定費」と「変動費率」になるのです。
ちなみに、先ほどの画像でも切片と傾き以外の数値がたくさんでてきていますが、このほとんどは結果の信頼性を表す数値です。欲を言えばこれらの数値も理解しておくことが望ましいですが、そもそもプロットがバラバラで固変分解する意味が薄いものは回帰分析しなければよいので、細かい部分は理解しなくてもよいと思います。重要なのは、切片と傾きの意味についてしっかりと理解することです。
以上、エクセルを使った回帰分析による固変分解について、例を交えながら説明しました。データ分析のノウハウは経営においても大きな武器になりますので、ぜひ身に付けて頂ければと思います。
[まとめ]
・ エクセル分析ツールを活用することで、非常に簡単に回帰分析を行うことができる
・回帰分析結果の「切片」は固定費を、「傾き」は変動費率をそれぞれ表している
会社経営や財務にお悩みの経営者や管理職の方、こちらのホームページからのご相談お待ちしております。
-1024x384.png)
-1024x386.png)





